Caesar-rejtjel

Hozzunk létre egy új projektet a blokkszerkesztőben!

1. lépés – Alapok lerakása: változók, szöveg másolása, eredmény kiírása

a) Hozzuk létre a változókat

uzenet – ebben van az, amit „titkosítani” fogunk (most: „Hello”).
eltolas_merteke – ennyivel fogjuk később eltolni a betűket az ábécében (most még csak előkészítés: 1).
titkos_uzenet – ide építjük fel az új szöveget (egyelőre csak lemásoljuk az eredetit).

Cél: legyen helyünk a kiinduló szövegnek, a későbbi eltolás mértékének, és legyen egy „üres dobozunk” az eredménynek.

b) Készítsünk egy függvényt, ahol a „titkosítás” lezajlik

Neve: titkositas().
Mit csinál most? Végigmegy a uzenet betűin egyesével, és hozzáfűzi őket a titkos_uzenet végéhez.
Vagyis: most még nem változtatunk a betűkön, csak átmásoljuk őket. Ez a biztonságos próba, hogy működik a „betűnkénti bejárás”.

Cél: megmutatni, hogyan lehet egy szöveget betűről betűre feldolgozni. A következő lépésben ide kerül majd a valódi eltolás.

c) Most az A gomb megnyomásával írjuk ki az új szöveget.

Ha megnyomod az A gombot, akkor:

lefut a titkositas(),
a micro:bit kiírja a titkos_uzenet tartalmát a kijelzőn.

Eredmény most: „Hello” → „Hello”.
Ez pont így jó: az alap működik, készen állunk arra, hogy a következő lépésben eltoljuk a betűket, és tényleg titkos legyen a kimenet.

2. lépés – Betűeltolás (Caesar) beépítése

Most, hogy már tudjuk betűnként végigmásolni az üzenetet, ideje előkészíteni a valódi titkosítást.
Ehhez két dolgot csinálunk: először kibővítjük a kódot, hogy minden betűnél legyen helyünk az átalakításra, majd megírjuk az eltolás függvényt, ami elvégzi a betűk „odébb tolását” az ábécében.

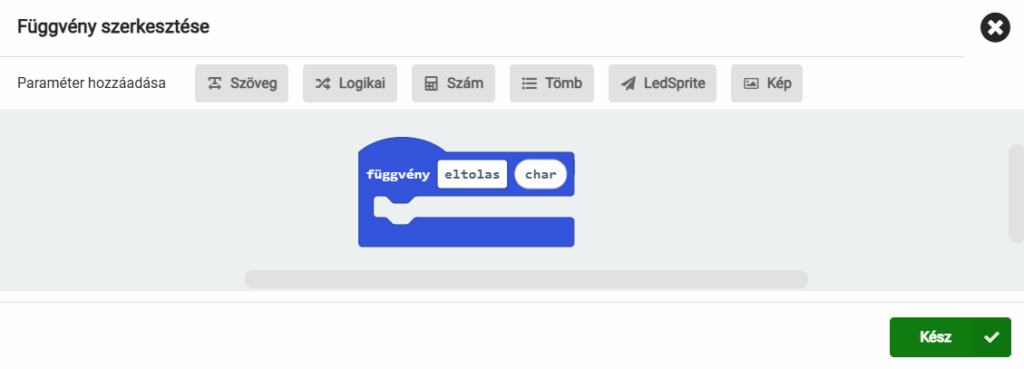
Mi változott az első lépéshez képest?

Bevezettük a temp változót: ebben tartjuk a soron következő betűt.
Létrehoztuk az eltolas(char) függvényt, ami most még üres. Ne felejtsd el hozzáadni a paramétert!
A titkositas() most minden betűt először a temp-be tesz, majd elküldi az eltolas() függvénynek, és csak utána fűzi hozzá az eredményhez.

Így a kód készen áll arra, hogy a betűt ne csak lemásoljuk, hanem tényleg átalakítsuk.

Mi az az ASCII? 🤔

Amikor a számítógép szöveget kezel, valójában nem betűket lát, hanem számokat.
Minden betűhöz, számhoz és írásjelhez tartozik egy egyedi számkód, amit a gép könnyen tárol és feldolgoz.
Ezt a kódrendszert hívjuk ASCII-nak (ejtsd: „ászki”).

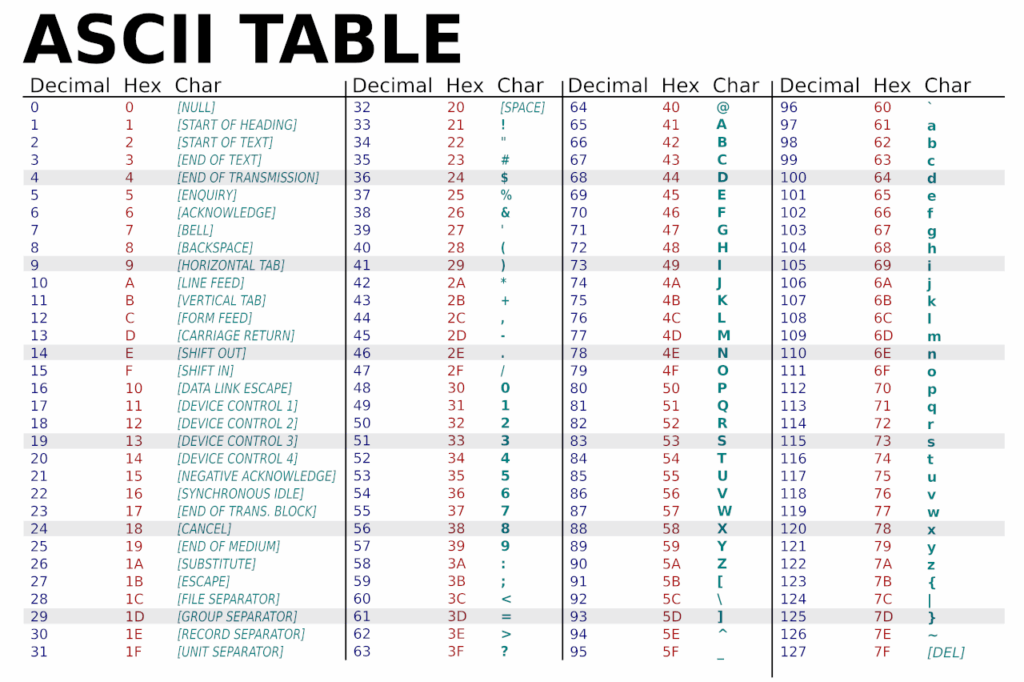
Hogyan működik?

Az ASCII megmondja, hogy melyik szám melyik betűhöz tartozik:

A → 65
B → 66
… egészen Z-ig (90).

A kisbetűk más számokat kaptak:

a → 97
b → 98
… egészen z-ig (122).

Más karaktereknek is van számuk, például:

szóköz ( ) → 32
! → 33
0 → 48

Hogyan használjuk a programban?

Ha azt írjuk: ASCII = char.char_code_at(0)

akkor a gép megmondja, milyen szám tartozik a betűhöz.

Ha pedig: temp = String.from_char_code(ASCII)

akkor a számot visszaalakítjuk betűvé.

Miért fontos ez a Caesar-kódhoz?

A Caesar-rejtjel lényege, hogy a betűket eltoljuk az ábécében.
Ez betűkkel nehéz lenne, de számokkal egyszerű:

B (66) + 1 = 67 → C

Z (90) + 1 = 91 → túlcsordulás! Ilyenkor levonunk 26-ot, így 65 lesz → A.

Így tudunk körbe-körbe lépkedni az ábécében.

🔎 Mit csinál ez a függvény?

ASCII = char.char_code_at(0) – minden betűnek van egy számkódja (A=65, B=66 … a=97, b=98 …). Ezt kérjük le.

Ha a betű nagybetű (65–90), akkor hozzáadjuk az eltolas_merteke értékét. Ha túlment a Z-n, levonunk 26-ot, hogy visszaugorjon az ábécé elejére.

Ha a betű kisbetű (97–122), ugyanezt tesszük, csak a kisbetűk tartományában.

temp = String.from_char_code(ASCII) – a számkódból visszavarázsoljuk a betűt.

Így bármelyik betűt képesek vagyunk „odébb tolni” az ábécében – most még 0 lépéssel, de hamarosan tényleges titkosításra is használjuk!

3. lépés – Mi van, ha túl nagy vagy negatív számot írunk? 🤔

Eddig minden szuperül működött, de gondolj csak bele:
mi történik, ha nem egy kicsi számot írsz eltolásnak, hanem mondjuk 27-et?
Hiszen az angol ábécé csak 26 betűből áll!

Legfontosabb kérdések:

Mi legyen, ha egy nagy számmal toljuk el a betűket?

Ilyenkor egyszerű a megoldás: újrakezdjük az ábécét.
Ha 26-ot lépsz, akkor pont visszaérsz ugyanoda.
Ha 27-et lépsz, az olyan, mintha csak 1-et lépnél.
Ha 52-t lépsz, az olyan, mintha 0-t lépnél.
Így mindig biztos, hogy a betűk nem futnak el valahová, ahol nincsenek betűk.

Na és mi legyen a negatív eltolással?

Előfordulhat, hogy nem előre, hanem hátra szeretnénk lépni.
Például: –1-et adsz meg eltolásnak.
Ez azt jelenti, hogy B helyett A jön, és az A helyett pedig átlépünk a végére:
- A → Z
- a → z
Így hátrafelé is tudunk titkosítani!

És mi van, ha elérjük az ábécé végét?

Mi történik, ha a Z betűn állsz, és még mindig előre kell lépni?
Nem baj! Ilyenkor átugrunk az elejére. Így lesz:

Z → A
z → a

Olyan, mintha egy körpályán mennénk körbe-körbe. 🚴‍♀️

Mi legyen, ha nagyobb számot írunk, mint az ábécé mérete? 🤔

A programban erre a modulo műveletet használjuk.
A modulo tulajdonképpen a maradékos osztás: azt mondja meg, mennyi marad, ha elosztjuk a számot 26-tal.

👉 Példa:

Ha az eltolás 27, akkor 27 mod 26 = 1, tehát ugyanaz, mintha 1-et lépnénk.
Ha az eltolás 52, akkor 52 mod 26 = 0, vagyis nem is mozdulunk el.

A kódban tehát minden eltolást eltolas_merteke % 26-tal kezelünk. Így a legnagyobb számok is szépen visszakerülnek a 0–25 közé, vagyis az ábécé betűi közé.

Mi legyen, ha elérjük az ábécé végét? 🚀

Ez már az előző lépésben is előjött: ha például a Z betűt 1-gyel eltoljuk, akkor az már 90 fölé csúszik a számkódban.

A programban erre egyszerűen figyelünk:

Ha nagybetűnél a szám nagyobb, mint 90 (Z), akkor levonunk 26-ot.
Ha kisbetűnél a szám nagyobb, mint 122 (z), akkor ugyanígy levonunk 26-ot.

Így a Z + 1 nem valami furcsa karakter lesz, hanem szépen visszaugrik A-ra.

Na és mi legyen a negatív eltolással? ↩️

Ha az eltolás negatív, akkor a betűk visszafelé indulnak az ábécében. Például A - 1.
Ilyenkor a szám kisebb lesz, mint az A kódja (65), vagy a kisbetűknél kisebb lesz, mint 97.

A kódban ezt egy ciklussal oldjuk meg:

Amíg a szám kisebb, mint a megengedett minimum, mindig hozzáadunk 26-ot.
Ez addig ismétlődik, amíg a szám újra bele nem fér az ábécé tartományába.